
无数游客都流连于杭州西湖之美,文人墨客也留下诗篇无数。27岁攻克数学几何难题、33岁获得菲尔兹奖(数学界的诺贝尔奖)的丘成桐先生眼里,向西看,“接天莲叶无穷碧,映日荷花别样红”,是许多重要而神秘的对称;向东看,“山外青山楼外楼”、“两峰相对不相连”,这种递归,是数学中无处不在的格点、分形,显示了对称美,也激发游人和数学家的发现未知的兴趣。因此,他曾填词一阙《几何美》,发出“穹苍广而善美兮,何天理之悠悠”感叹。
数学之美无处不在,从数学史的发展来看,“零”等数字从古老的计数方式中诞生,无理数、素数、拓扑等创新打开了人类对未知世界的进一步探索。日前,中国科学院院士、美国艺术与科学院院士、北京大学讲席教授田刚,娓娓道来,以《数学之美》为主题来解析数学中诸多有用之美与无用之力,听完人类数千年数学的发现之旅,你会不知不觉爱上数学。

中国科学院院士、北京大学讲席教授田刚讲述数学之美
无数不在的数学之美
数学无处不在,具有巨大冲击力的是数学之美。田刚如数家珍,从大自然、建筑到艺术,无一例外。
一般人也许不太留意向日葵,向日葵花瓣有21个深蓝色螺旋线和13个宝石绿螺旋,13和21是斐波那契数列中的相邻数字。莱昂纳多·斐波那契是12世纪至13世纪的意大利数学家,他发现了一串数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始,每一项都等于前两项之和,这也被称为黄金分割数列,在现代物理、准晶体结构、化学等领域,都有直接的应用。“大自然似乎在人类之前,就发明了数学”,田刚笑称。

向日葵花瓣有21个深蓝色螺旋线和13个宝石绿螺旋
无独有偶,在达芬奇的名画《蒙娜丽莎》《最后的晚餐》里,充满了黄金分割数列。而在《最后的晚餐》里,12个门徒分成3组,每组4人,对称地分布在基督两边,基督本人被画成一个等边三角形,这样的目的在于,“表达基督的情感和思考,并且身体处于一种平衡状态”。
在建筑中,田刚非常推崇伊朗的伊斯法罕城里的谢科洛夫拉清真寺的房顶,它建于在17世纪,花了17年,上面的窗口有光线,仰看时如同孔雀开屏,但方向能始终对着圣地麦加,因此需要精确的计算,其上有着双螺旋图案。这是阿巴斯一世请其岳父,是黎巴嫩非常著名的伊斯兰教学者,被请来主持清真寺和神学院工作,“当时也算是人才引进”。
几何密铺古人用过很多,西班牙格拉纳达红宫是伊斯兰世界在西班牙留下的辉煌古迹。采用各种几何图形的对称、旋转、平移来装饰。目前存在的17中类型的几何密铺在红宫里都能找到。

谢科洛夫拉清真寺的房顶,其上有着双螺旋图案
数学如何诞生并发展
数学起源于人类早期的生产活动,等到数字的发明成熟后才有了数学这个学科。
*三种计数方法的发明:二进制、十进制、六十进制
早期以实物计数,古代文明中,有不同的计数方法。公元前8000年,牧羊人出去,用陶筹计数,有考古学家认为,陶筹与契形文字有关系。苏美尔人迁徙到西亚的两河流域,乌鲁克泥板上就有记载。
现存的计数法中有三种,现代社会,二进位法被广泛使用,如计算机和二维码。古代中国和古埃及都使用十进位法。在美索不达米亚平原则使用六十位法。
在古巴比伦,钉头型代表1,尖头型代表10。从60起使用符号组,记录60的符号也是由之前的符号构成。古巴比伦数学在当时非常先进,在代数领域,可解有三个未知数的方程式,并有简单的三角函数表。在柏林佩加蒙博物馆,陈列着古巴比伦伊什塔尔城门,就是依据原件同比例复原所成,其中充满着数学知识。
六十进制至今仍被使用,如被应用于时间的计数,六十秒等于一分钟等;圆周也分为360度。田刚夸奖苏美尔人很有想象力,右手除大拇指外的四个手指均有三段指节,满12后把左手小指拳起来,以此类推。这样就可以用来计数。
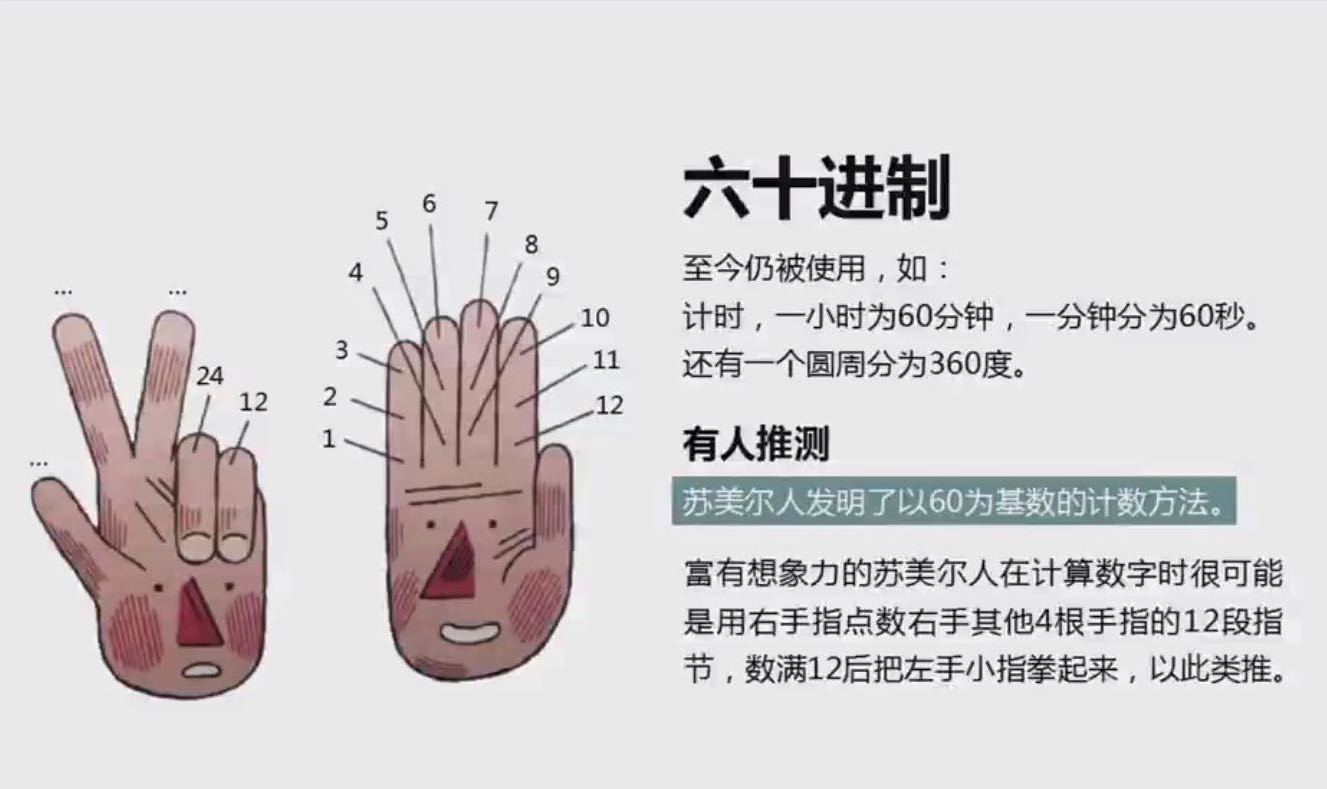
六十进制至今仍被使用,如被应用于时间的计数
*阿拉伯数字原来是印度人在公元前三世纪发明
公元前3世纪,数字获得了新的生命形式。在古希腊哲学家探寻世界本原时,毕达哥拉斯提出“数是万物之本”,数字从具体物品中、从现实中抽离了出来。
最初提到自然数字,指1,2,3,4,5,6,7,8,9……虽然我们称它们为“阿拉伯数字”,但其实是印度人在公元前三世纪发明,再根据位置原则确定个位、十位、百位。公元700年,阿拉伯学者在被征服的印度,收获了古印度人的先进的数字发明,阿拉伯数字极为简化,带来了便捷,此后,阿拉伯人又打到了欧洲,欧洲人很长时间对阿拉伯数字视而不见,固执地使用比较费事的罗马数字。意大利大数学家斐波那契在欧洲大力推广阿拉伯数字,一直到13世纪,印度阿拉伯计数法才慢慢在西方推广开来 。
*零是数学史上伟大发明,打开了通向负数之门
古印度人发明了1至9,那么零又是怎么出现的呢?田刚分享了一段趣闻。2014年世界数学大会在印度举办,印度学者在主持会议时说,印度对数学的贡献在于零,零是印度人发明的。无就是零,意识到零是一个数字,是一个大突破。此前所有的数字都是尺子能量出来的,但尺子量不出零,抽象概念有所突破。公元5世纪,印度人发明了零,在1-9发明了一千年后,发明了零,最早是用点来表示。“零是数学发展史上最伟大的发明之一,零打开了通向负数的大门”,田刚给予了高度的评价。
早在两千多年前,我国就有了正负数的概念,比埃及、印度早六七百年,比欧洲则早了一千多年。在古代数学书《九章算术》中就称正负数的计算为“正负术”,魏晋数学家刘徽说:“正算赤,负算黑;否则以邪正为异” 。传说欧洲人一直把零视为荒诞之事,直到十五世纪才接受。田刚讲述了英国数学家德摩根在1832年仍认为负数为虚构的故事。比如:父亲56岁,儿子29岁,何时父亲的年龄是儿子的两倍?如果用方程式解,结果这个X就是-2,他认为这是荒唐的。在中文世界里非常容易理解,就是时光倒回2年,父亲年龄就是儿子的2倍;又比如(-2)+(-5)是-7。这些概念在今天看来很简单,但在历史上,是经过长时间人们的认识后才得出的。

《九章算术》是中国古代数学专著
*希伯索斯发明无理数,因此付出生命代价
毕达哥拉斯认为,数必须用整数和整数的比表达的,即是有理数。在公元前500年,他的弟子希伯索斯发现了一个惊人的事实,若正方形的边长为1,对角线为根号2,这不是一个有理数。这一发现与毕达哥拉斯的理论大相径庭,这使得学派领导人大为惶恐,认为这将动摇他们在学术界的崇高地位,于是竭力封锁了真理的传播,希伯索斯被迫流浪他乡。一日被毕氏手下门生撞见,残忍地将他扔到了大海里。希伯索斯失去了生命,但发现的无理数依然流传至今。常见无理数有圆周率π,欧拉数e,黄金比例。
接着不断有新的数字被发明。田刚举例:有理数和无理数放在一起就形成了实数。16世纪时,大家意识到,代数方程求解,出现了i的平方根,法国数学家、哲学家笛卡尔(1596-1650)给出了 “虚数”这个名称,表示“-1的平方根”。随着科学的发展,虚数在水力、绘图、航空等领域中得到了广泛的应用。第一个引入复数的是意大利科学家卡尔达诺,他在1545年给出了一元三次方程的一般解法,被称为“卡当公式”。
*《几何原本》中,欧几里得严格论证了勾股定理
公元前300年,欧几里德完成了《几何原本》。全书分13卷,有5条“公理”或“公设”,23个定义和467个命题。该数在印数比肩《圣经》和《可兰经》。欧几里得严格论证了勾股定理:3的平方+4的平方=5的平方,即中国古人所言“勾三股四玄五”,这也是毕达哥拉斯定理。田刚告诉听众,古代没有很多测量工具,可以通过勾股定理得出直角。
*哥德巴赫猜想、黎曼猜想都和素数相关
《几何原本》里还含有很多数论。数论是数学的核心分支之一,是研究素数的一个重要部分。

1896年,阿达马和瓦莱布桑各自独立证明了素数定理
许多著名的猜想都与素数有关,如,被誉为“皇冠上的明珠”的哥德巴赫猜想:任何一大于2的偶数都可写成两个素数之和。田刚说,“至今最好的结果是1966年陈景润先生证明的。”还有很著名的黎曼猜想也要用到了素数,但“目前还不是一个数学定理。”谈到这里,田刚提出了较为深刻的定理——素数定理。1896年,阿达马和瓦莱布桑各自独立证明了素数定理;1949年,塞尔伯格和埃尔德什分别独立地给出了素数定理的完全“初等”的证明。该定理意在告诉你一个素数的分布,一千个素数看不出规律,增长后就有规律。除了5以外,大于5以后,不能以5结尾的数字,几乎都是奇数,以9结尾的数字和以1结尾的数字各占20%。
*素数奠定了现代信息的基本安全,广泛用于密码学
尽管这个定理有些深刻,但素数是现代信息安全技术的基础。密码学广泛应用在日常生活中,包括自动柜机的芯片卡、电脑使用者存取密码、电子商务等等。在电子商务里,密码学中经典的RSA算法被广泛使用。信用卡使用的RSA密码,有包含200位数的超大数字之和。田刚提醒,现在看来扫码非常便捷,但其安全性其实并没有刷卡高。
又如,在好莱坞电影《超时空接触》,片中主人公坚信,太阳系里一定还有其他星球有生命。他收到一个信号,但无法破解,最后主人公利用素数的数学理论破译了密码。田刚解释,这说明语言有时行不通,只有素数可以和外星空沟通。这部电影是依据康奈尔大学物理系教授的小说所改编。

好莱坞电影《超时空接触》
*怀尔斯终于证明了费马大定理,椭圆曲线被广泛应用
数学发展中,更多数被引进,如由椭圆曲线定义的抽象数。1621年,著名的费马大定理就和此有关,费马声称自己有一个“绝妙的证法”,但没有写下来。费马猜想在1994年被英国著名数学家、牛津大学教授怀尔斯所证明。提到这位曾经的普林斯顿大学同事,田刚非常佩服,因为历经七年研究消息公布后,被人发现有一个小BUG,这意味着怀尔斯并没有解决费马大定理,压力之大可想而知,“但他能沉下心来,花14个月将此完善,真正论证了费马大定理。”田刚说,怀尔斯在日常生活里非常谦虚,怀尔斯的证明用到了大量的现代数学工具和技巧,证明揭示了椭圆曲线和数轮之间的深刻联系。费马大定理的证明被全世界公认为是20世纪伟大的数学成就之一。
这几年,利用椭圆曲线的密码系统越来越受到重视。救生圈的表面就是三次曲线的几何的实现。

英国著名数学家、牛津大学教授怀尔斯论证了费马大定理
数学不以“有用”为研究原点,实际非常有用
田刚在2014年就提出,数学不以“有用”为研究的原点,“但实际很有用。”时隔6年他强调。复数、虚数的引入一开始是为了学术研究,但现在发现电路等都需要用到。
爱因斯坦广义相对论,引力场就是很大的弯曲,光线在太阳附近经过时,空间就会弯曲。1919年被日全食时验证了。人们看到太阳后面的东西。
2016年诺奖物理学奖颁发给了三位从事拓扑相变和拓扑物质形态研究的学者。拓扑物质相态用拓扑示性数,比如“陈数”,来刻画新的物质形态。拓扑相还存在于三维材料中,有望在新一代电子器件和超导体中产生应用,以及在未来量子计算机方面应用。1993年,田刚和阮勇斌首次建立了计数几何的数学理论,解决了一类经典的计数几何问题。
数学在经济学、生物学等学科中的发展中同样起到了非常重要的作用。田刚例举了一串曾是数学家的诺奖经济学奖获得者:《美丽心灵》的主人公约翰·纳什为1994年获得者;1997年得主罗伯特·莫顿是数学家;2005年获主罗伯特·奥曼的最高学历是MIT的数学博士;2012年获奖的罗斯和沙普利,在本科和博士读的都是数学专业。
当前最热的人工智能,有观点认为,其本质就是数学,而大数据,本质上就是海量数据的汇集。田刚分析,二维码早期是一维条码,二维码能储存更多信息,矩阵式二维码是日本人发明的。QR码能放入1817个汉字,7089个数字、4200个英文数字。
因此,数学是自然科学的基础,其基础性、引领性使得它在科学研究和国家发展中处于核心地位。

2016年诺奖物理学奖颁发给了三位从事拓扑相变和拓扑物质形态研究的学者
1687年,牛顿发表了《自然哲学的数学原理》,数学的领先成果促进了工业革命,英国一跃成为超级强国;二战后,应罗斯福总统要求,万尼瓦尔·布什完成了《科学:永无止境的边疆》的报告,提出科学将成为推动国家发展的新动力,并带来广泛的利益。反观中国,近年,国家印发了《关于加强数学科学研究工作方案》,这是史无前例的。新兴的融合学科开始建立,优秀的中青年数学家成长了起来。
“天道几何,万品流形先自得;变分无限,孤心测度有同伦。”田刚以北京大学国际数学研究中心门口的一幅对联再次将听者的诸多的兴趣点燃,这里面藏着不少数学术语。
作者:李念
编辑:袁琭璐
责任编辑:李念
*文汇独家稿件,转载请注明出处。





